Traslazione
Cominciamo con l’operazione di spostare la figura lungo una direzione, come se scorresse su binari paralleli.DEFINIZIONE Chiamiamo vettore un segmento sul quale
abbiamo stabilito un orientamento. Un vettore è caratterizzato da 3
grandezze: ampiezza (la lunghezza del segmento), direzione (la
retta a cui appartiene il segmento), verso (l'ordine con cui ci si
sposta sulla retta direzione). 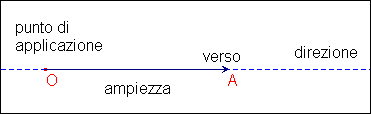 DEFINIZIONE Due vettori che hanno uguali ampiezza, direzione e verso si dicono fra loro equipollenti. |
Quindi, fissato un punto del piano o dello spazio, il vettore è un segmento che ci indica di quanto, in che direzione e in che verso ci dobbiamo spostare, mediante la sua ampiezza, la retta a cui appartiene e l’ordine su di essa stabilito. Possiamo perciò dire che un vettore è individuato dalla sua ampiezza, dalla sua direzione e dal suo verso.
Spesso nel linguaggio comune si parla di distanza in linea d’aria. Per esempio se dobbiamo spostarci da casa nostra al centro della città, diciamo che in linea d’aria questo è un percorso per esempio di 1 chilometro. Ciò significa che, se consideriamo il percorso più corto possibile, appunto quello che si effettuerebbe volando senza ostacoli di alcuna natura, dovremmo percorrere Km 1. In realtà nel nostro percorso siamo vincolati a seguire le strade tracciate, se andiamo con un mezzo siamo anche limitati dai divieti di circolazione e così via.
Se però consideriamo il segmento orientato da casa (punto di partenza) al centro (punto di arrivo) e lungo 1 chilometro otteniamo il vettore che rappresenta il percorso minimo, anche se solo teorico.
Anche se potrebbe sembrare ovvio è importante definire
anche il concetto seguente.
| DEFINIZIONE Diciamo vettore nullo il vettore che applicato a qualsiasi punto del piano gli associa lo stesso punto. |
In effetti lo stare fermi è un tipo molto particolare di movimento, appunto il movimento nullo. Ce ne rendiamo meglio conto dall’osservazione fisica di un corpo in movimento. Anche se il corpo rimane fermo, da un punto di vista fisico qualcosa sta variando: il tempo.
Passiamo adesso a definire la prima isometria che vogliamo trattare.
DEFINIZIONE Diciamo traslazione di vettore v la trasformazione geometrica t che a ogni punto P associa il punto P + v. Cioè in formula: t (P) = P + v |
Il famoso screen saver Testo scorrevole è un classico esempio di traslazione.

Enunciamo il seguente risultato abbastanza intuitivo.
TEOREMA Una traslazione è una isometria. TEOREMA In una traslazione
|
Una volta
che siamo passati da un punto a un altro ci potrebbe interessare fare il
contrario,
andati in centro vogliamo ritornare a casa. Per far ciò abbiamo
bisogno di definire un altro
concetto.
DEFINIZIONE Dato un vettore v , diciamo suo vettore opposto, quel vettore che ha la stessa ampiezza di v , la stessa direzione ma verso opposto. Il vettore opposto di v lo indichiamo con il simbolo – v . |