Rotazione
Un altro tipo di movimento rigido è la rotazione. Essa può farsi in due versi, o come girano le lancette dell’orologio o nel verso contrario. Per convenzione scegliamo come verso di rotazione quello contrario alle lancette dell’orologio, detto anche antiorario.
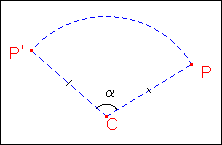
DEFINIZIONE Diciamo rotazione di centro C e angolo a la trasformazione geometrica che a
ogni punto P associa il punto P', ottenuto considerando la
circonferenza G di centro C e
raggio CP e l’angolo a di
vertice C, un lato del quale è la semiretta CP. Il punto P'
è ottenuto dall’intersezione dell’altro lato dell’angolo con G.
| Da un punto di vista per così dire pratico, la rotazione di un certo punto si effettua puntando il compasso sul centro della rotazione e, con l’apertura che va a toccare il punto, spostando il compasso di un angolo uguale a quello della rotazione. Anche in questo caso enunciamo e dimostriamo un risultato relativo all'isometria della trasformazione. |
TEOREMA Una rotazione è una isometria.
TEOREMA Una simmetria centrale di centro O equivale a una rotazione di un angolo piatto, sempre di centro