|
Incontro
tra topi
Il problema matematico dei topi consiste nel determinare la traiettoria
di n topi, posti ai vertici di un poligono di n lati, di lunghezza
unitaria, e il loro punto di incontro, ipotizzando che ogni topo si
dirige verso il compagno più vicino, muovendosi in senso antiorario
e a velocità costante.
Ogni topo traccia una
spirale logaritmica: tutti i topi si incontrano nel centro
del poligono e percorrono una distanza, dipendente dal numero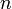 
dei lati del poligono, pari a
|
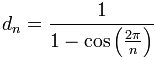
Se n=2
la spirale degenera in una retta; i topi, posti agli
estremi del segmento, si incontrano nel punto medio del
segmento
 
|
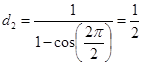
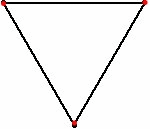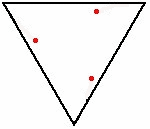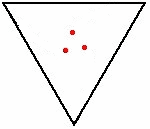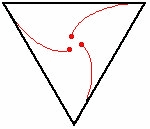
Se n=3
i topi, posti ai vertici di un triangolo, si muovono lungo
una spirale logaritmica e si incontrano nel centro del
triangolo. Lo spazio percorso è
 |
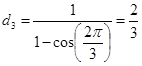
Se n=4, i topi posti ai vertici del quadrato
 |
|
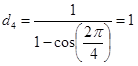
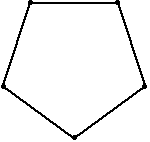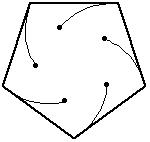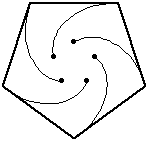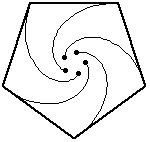
Se
n=5, i topi posti ai vertici del pentagono
|
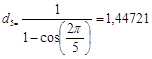
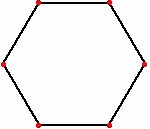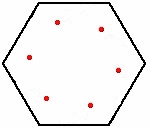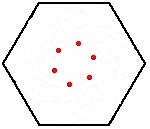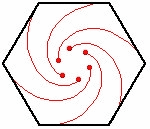
Se
n=6, i topi posti sui vertici dell’esagono, tracciano una
spirale logaritmica e si incontrano nel centro del poligono.
La distanza percorsa è
 |
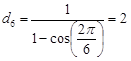
Osservazioni
Il problema può essere generalizzato,
considerando poligoni non regolari, o topi che si muovono a
diverse velocità e con punti di partenza diversi.
|
Curiosità
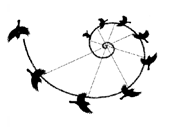
Il falco, uno
dei predatori più temibili per la vista acuta e l’abilità di
volo,
nel piombare su una preda non sceglie una traiettoria rettilinea,
più breve e più veloce, ma segue una
spirale logaritmica.
Per la posizione e la natura dei suoi occhi, quando è in volo, il falco ha
una direzione visiva privilegiata che forma un certo angolo con la
sua direzione di volo: l’angolo di inclinazione della spirale.
Infatti, per vedere la preda, il falco dovrebbe ruotare la
testa, peggiorando la sua aerodinamica, mentre seguendo una spirale
logaritmica non perde di vista la preda e massimizza la velocità.
|
 |
|
