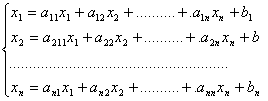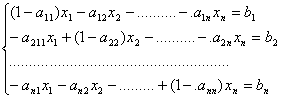|
Modello economico di Leontief
Una tra le più
eleganti e utili applicazioni della teoria delle
matrici e dei
sistemi lineari è il
modello lineare
a produzione
semplice dell’economista americano, di origine russa, Wassily
Leontief.
Un modello lineare di produzione coinvolge n beni ed n imprese, ogni
impresa, nella sua attività produttiva, necessita di alcuni beni per
produrne altri: i fattori produttivi sono detti inputs
mentre i beni prodotti sono detti outputs.
Leontief asseriva che occorre interpretare la realtà
economica in termini della sua struttura (tecnologie, stili di vita
consumi, risorse primarie) mediante uno strumento contabile - la
tavola input-output, o tavola delle interdipendenze
settoriali, che consente una descrizione delle relazioni tra le
quantità di beni prodotte e consumate.
Leontief elaborò un particolare modello lineare a produzione
semplice, detto modello di analisi intersettoriale o,
analisi input/output I/O, per il quale gli fu conferito nel
1973 il premio Nobel per l’economia, formulando alcune
ipotesi semplificatrici:
- l’economia nazionale è costituita da n imprese interagenti
tra loro;
- ogni impresa produce un solo prodotto e usa un solo processo
di produzione, per cui deve acquistare prodotti
da altre imprese;
- ogni impresa vende i propri prodotti alle altre imprese e a
eventuali consumatori;
- il livello di produzione xi deve essere sufficiente a
soddisfare la domanda di input delle n imprese e anche la
domanda finale dei consumatori
La tavola Input – Output, è una matrice a doppia entrata costituita
da tre sottomatrici:
-
la sottomatrice settore-settore,
è una matrice
quadrata in cui ad ogni riga ed ad ogni colonna
corrisponde un settore di produzione omogenea, e nella quale le
colonne registrano i flussi di beni e servizi che ciascun
settore acquista da tutti gli altri, mentre, le righe registrano
i flussi che ciascun settore vende a tutti gli altri;
-
la sottomatrice degli impieghi
primari e delle risorse evidenzia il valore aggiunto e le
sue componenti, quali retribuzioni, oneri sociali, imposte,
produzioni, importazioni. Le righe della sottomatrice
rappresentano i costi e le risorse, mentre le colonne mostrano
le branche;
-
la sottomatrice degli
impieghi finali, registra i flussi finali tra settori e domanda finale.
La lettura della matrice I-O nel senso delle colonne consente di
analizzare per ciascun settore, la struttura dei costi di
produzione; i totali di ogni colonna, rappresentano gli acquisti
effettuati da ciascun settore.
Leggendo la matrice nel senso delle righe, invece, è possibile
analizzare la produzione dei settori, i totali di ogni riga
rappresentano, le vendite realizzate da ogni settore.
La matrice intersettoriale permette di determinare la matrice
dei coefficienti tecnici 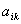 , che
esprimono la quantità del bene i-esimo necessaria per produrre
un’unità del k-esimo bene, dividendo ogni elemento di ciascuna
colonna, che rappresenta il bene, per la produzione lorda.
Il modello di Leontief, è costituito dal seguente sistema lineare,
le cui equazioni esprimono la domanda totale degli n produttori
|
 |
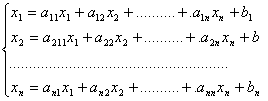Trasportando a primo membro i termini in xi si ha:
 |
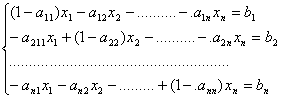La forma matriciale del
modello di Leontief è : (I-A) X = B , dove I è la matrice unitaria;
X è il vettore colonna delle quantità prodotte; A è la matrice dei
coefficienti tecnici e B è la matrice dei termini noti
Osservazioni:
-
se
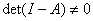  esiste
la sua matrice
inversa e si ricava 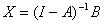 . Questa
forma di risoluzione permette di determinare le soluzioni al
variare del vettore B della domanda finale, in relazione a varie
programmazioni economiche, evitando di risolvere ogni volta il
sistema;
-
la matrice si caratterizza per la presenza di valori
superiori all’unità lungo la diagonale principale mentre gli
altri elementi sono tutti inferiori all’unità ;
-
per la risoluzione del sistema devono essere
soddisfatte le seguenti condizioni:
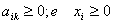 ossia
i coefficienti delle incognite e le soluzioni devono essere non
negativi;
-
la significatività economica delle soluzioni sia del
modello delle quantità sia del modello dei prezzi dipende dalle
caratteristiche della matrice (I - A)-¹, detta anche 'inversa
di Leontief' o matrice dei fabbisogni diretti e indiretti di
produzione;
-
la matrice inversa di Leontief consente il calcolo dei
moltiplicatori settoriali:sommando i valori per colonna si
ottiene l’incremento di produzione determinato da un incremento
unitario della domanda finale per il settore economico
intestatario della colonna.
Utilità del modello
Il modello di Leontief è utile come strumento di previsione:
- ipotizzando la previsione dei consumi futuri e disponendo della
matrice dei coefficienti tecnici, la soluzione del sistema permette
di formulare una previsione delle quantità da produrre in ciascun
settore;
- al variare della domanda da parte degli utilizzatori finali, il
modello permette di analizzare quali mutamenti si verificano nei
diversi settori produttivi.
Il modello input-output si presenta come un modello di
ottimizzazione di solito risolto con le tecniche della
programmazione lineare. |
