|
Matrici di Leslie
Le
matrici di Leslie (dal nome del biologo che negli
anni '40 le utilizzò), o matrici di previsione di una popolazione,
rappresentano un’applicazione della teoria delle
matrici alla
demografia (disciplina che studia i modelli secondo cui si sviluppano le popolazioni umane o animali).
La formalizzazione del modello, utilizzato da Leslie, richiede l’introduzione di ipotesi semplificatrici:
- la popolazione è chiusa, ossia non è contraddistinta da flussi migratori da e verso l’esterno;
- i tassi di natalità e di sopravvivenza sono costanti nel tempo;
- si studia soltanto la parte femminile della popolazione.
Ipotizzata una popolazione di insetti aventi le seguenti caratteristiche:
- la durata della vita sia non superiore a 3 mesi;
- metà degli insetti superi il 1° mese, ma solo un quarto di questi raggiunga il 2° mese;
- da ogni insetto nel 2° mese si generino 4 nuovi insetti e nel 3° mese si generi
un nuovo insetto, i dati si possono rappresentare in una matrice
di 3 righe e 3 colonne, in cui la prima riga indica la fertilità,
la seconda la probabilità che un insetto di età zero
sia in vita almeno fino al compimento di un mese, nella terza
riga la probabilità che un
insetto di un mese sia in vita fino al compimento di 2 mesi:
|
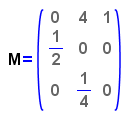
Esempio
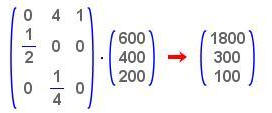
una popolazione di insetti, costituita da 600
insetti del primo gruppo (ossia con meno di un mese di vita), 400
insetti del secondo gruppo (ossia nel secondo mese di vita), 200
insetti del terzo gruppo (ossia nel terzo mese di vita) si può
rappresentare con la matrice: |
 |
L'evoluzione della popolazione degli insetti nei vari mesi si calcola mediante il prodotto M∙
P.
Osservazioni
-
il calcolo matriciale permette di
determinare rapidamente come si modificano i tre gruppi di
insetti al passare del tempo, ferma restando la matrice di
trasformazione;
-
in generale, se i gruppi di età sono n
si ha una
matrice quadrata di ordine n
|
