Somma di matrici: assegnate le matrici

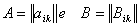
la matrice somma si ottiene addizionando i termini di uguale indice

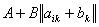
Osservazioni:

• la somma tra matrici è possibile solo se le matrici hanno uguali dimensioni;

• nel prodotto tra matrici la proprietà commutativa vale solo se le matrici sono quadrate dello stesso ordine e una di esse è scalare, oppure una di esse è la matrice unitaria;

• il prodotto di una matrice per la sua inversa dà come risultato la matrice unità

Prodotto di una matrice per uno scalare: assegnati una matrice e un numero reale, la matrice prodotto per uno scalare è una matrice che si ottiene moltiplicando tutti gli elementi della matrice per tale numero.

Prodotto tra matrici (prodotto righe per colonne): assegnate due matrici tale che il numero delle colonne della prima (n*r) sia uguale al numero delle righe della seconda (r*m), la matrice prodotto è uguale alla somma dei prodotti degli elementi della riga i-esima di A per gli elementi corrispondenti della colonna k-esima di B, ossia
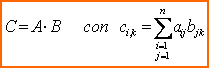