|
Matrice
associata ad una conica
Ad una qualsiasi
funzione di 2° grado si può associare un’opportuna
matrice che
permette di stabilire il tipo di conica. L’equazione di
una conica si può scrivere:

La matrice
associata alla conica è
la matrice
simmetrica di ordine 3
 |
Osservazione
Lo studio geometrico delle coniche e la loro classificazione può
essere ricondotto allo studio delle matrici simmetriche di ordine 3.
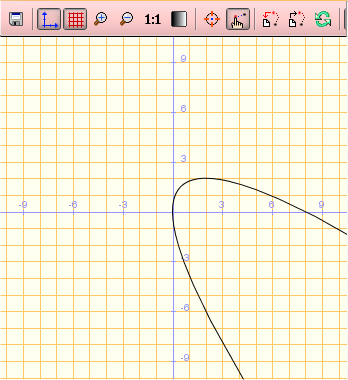
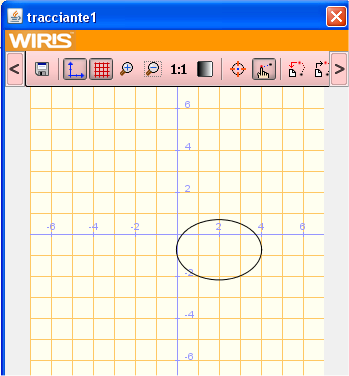
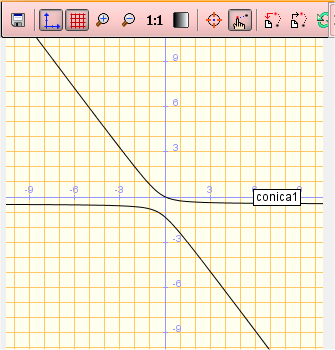
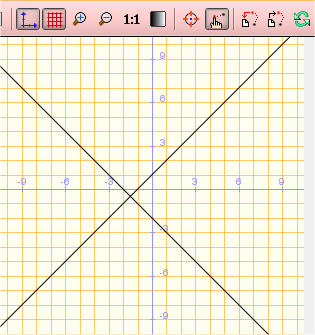
TEOREMA: esistono quattro tipi di coniche: ellisse,
parabola, iperbole e conica degenere, formata dal prodotto di due
rette.
|
Minore
principale di una matrice di ordine n é il
determinante di ordine k è
costituito dalle prime k righe e colonne.
TEOREMA: una conica non degenere è:
-
un’elisse se il minore
principale di ordine 2 è > 0;
-
una parabola
se il minore di ordine 2 è = 0;
-
un’iperbole se
il minore di ordine 2 è < 0
TEOREMA: una
conica è di tipo degenere se, e solo se, il determinante
della matrice associata è nullo.
|