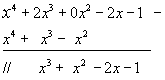Il concetto di multiplo e divisore fra polinomi è analogo a quello formulato per i monomi. Più difficile è invece operare con essi, per esempio semplificare una frazione algebrica polinomia.

Abbiamo già visto che le lettere di un polinomio e, più in generale, di un'espressione letterale, rappresentano numeri, pertanto dividendo due polinomi ci aspettiamo di dovere utilizzare procedimenti e di ottenere dei risultati in qualche modo simili a quelli ottenuti o utilizzati nella divisione fra due numeri. Sappiamo che dividendo due numeri interi, di cui il secondo diverso da zero, otteniamo due numeri interi: il quoziente e il resto. Inoltre il quoziente è un numero minore o uguale del dividendo, mentre il resto è sempre minore del divisore. Per ottenere analoghi risultati nella divisione fra polinomi dobbiamo definire in essi una relazione di ordine, che ci permetta di stabilire quale dei due polinomi sia maggiore dell'altro. Nel caso in cui i polinomi sono nelle stesse variabili, possiamo dire che è maggiore chi ha grado maggiore.

Questa osservazione ci permette di accettare il seguente fondamentale risultato, che non dimostreremo e che è simile all'analogo risultato nella divisione fra due numeri interi.

Teorema 1.
Dati due polinomi nelle stesse variabili, f e g, con f che ha grado maggiore o uguale a quello di g, esistono e si possono determinare in modo unico due polinomi q e r, che soddisfano le seguenti proprietà:

· il grado di r è minore di quello di g;

· il grado di q è uguale alla differenza fra il grado di f e quello di g;

· f = q × g + r.

Vediamo con un esempio come si possano determinare quoziente e resto della divisione fra due polinomi. I ragionamenti che faremo sono validi per qualsiasi coppia di polinomi, col polinomio dividendo di grado maggiore o uguale del polinomio divisore.

Vogliamo dividere x⁴ – 2x + 2x³ – 1 per x² – 1 + x. La prima cosa da fare è ordinare i due polinomi: cercando un'analogia tra polinomi e numeri potremmo dire che tale necessità è dovuta al fatto che il grado di ogni termine del polinomio è in qualche modo il corrispondente della posizione che una cifra occupa in un dato numero. Abbiamo perciò

Osserviamo poi che se i polinomi non sono completi dobbiamo completarli. Anche in questo caso c'è un'analogia con i numeri. In un numero le eventuali cifre uguali a zero sono importanti come le altre: ad esempio i numeri 23 e 203 sono diversi fra loro, perché la cifra 0 in 203 rende il 2 di valore 200, mentre la sua mancanza, in 23, lo rende di valore 20.

Si ha quindi

Adesso possiamo cominciare a dividere. Come dobbiamo procedere? In modo analogo a come si fa con i numeri, basta dividere fra loro i monomi di grado maggiore. Avremo così

Adesso moltiplichiamo questo risultato per il polinomio divisore:

Sempre in accordo con quanto effettuato con i numeri, sottraiamo questo risultato dal polinomio dividendo:

Possiamo eseguire il tutto con uno schema di divisione classico:

in cui, per semplicità di calcolo, abbiamo cambiato i segni al polinomio prodotto calcolando così una somma anziché una differenza.

A questo punto possiamo continuare la divisione con un procedimento analogo: eseguiamo dapprima la divisione tra il primo termine del resto parziale per primo termine del divisore, per ottenere il secondo termine del quoziente, cioè:

moltiplichiamo il secondo termine del quoziente per il polinomio divisore, sommiamo tale prodotto, cambiato di segno, e così via.

Nella divisione fra numeri arrestiamo la divisione quando il resto è minore del divisore, nei polinomi quando il grado del polinomio resto è minore di quello del polinomio divisore. E in questo caso abbiamo ottenuto un polinomio di grado inferiore a quello del divisore, quindi possiamo dire di aver finito. Il quoziente della divisione è perciò x² + x, il resto –x – 1.

Verifichiamo che la divisione è stata eseguita correttamente.

Tenuto conto dell'esempio enunciamo il seguente risultato.

Teorema 2
Dati due polinomi f e g, nelle stesse variabili, con f che ha grado maggiore o uguale a quello di g, detti q ed r rispettivamente il polinomio quoziente e il polinomio resto della divisione di f per g, si ha:

f/g = q + r/g

Osserviamo che la divisione serve non tanto per ridurre ai minimi termini una frazione algebrica polinomia, ma a trasformarla nella somma di un polinomio e di una frazione algebrica ridotta ai minimi termini.