Indici centrali
Affrontiamo adesso la questione più importante. Dopo aver raccolto i dati e averli rappresentati bisogna analizzarli. Cerchiamo di rappresentare l’intera distribuzione statistica con un solo valore.
DEFINIZIONE Data una distribuzione statistica a valori numerici, chiamiamo suo indice centrale un elemento che rappresenti tutte le sue modalità. |
Riprendiamo l’esempio degli occupati in Italia in un certo periodo di tempo, che riportiamo di nuovo.
Anno |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
Occupati |
23 476,9 |
22 736,4 |
22 495,4 |
22 487,7 |
22 563,5 |
22 661,0 |
22 870,1 |
Anno |
1999 |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
Occupati |
22 994,7 |
23 412,3 |
23 828,6 |
24 132,2 |
24 282,9 |
24 294,1 |
24 192,2 |
Possiamo dire quanto è stato, in media, il numero di occupati in Italia nel periodo 1992 – 2005?
Cosa vuol dire in media? Ecco il primo problema da risolvere. Un primo modo consiste nel "fare finta" che il numero di occupati sia rimasto sempre lo stesso nei 14 anni, quindi nel suddividere in parti uguali il totale dei 14 anni.
DEFINIZIONE Data una distribuzione statistica numerica di cardinalità finita diciamo media aritmetica delle sue modalità il numero ottenuto dal rapporto fra la somma delle modalità e la loro cardinalità totale. |
Possiamo quindi dire che la media di occupati in Italia nel periodo 1992 –2005 si ottiene dividendo il totale di 326 428 per 14, cioè circa 23 316,286.
A volte la media aritmetica deve tenere conto delle frequenze con cui ciascun dato si presenta. Supponiamo per esempio che la tabella seguente si riferisca all'altezza dei ragazzi di una classe.
Altezza (in cm) |
168 |
169 |
170 |
171 |
172 |
Numero di studenti |
3 |
4 |
4 |
2 |
5 |
Qual è l'altezza media della classe? Non è detto che sia 170 cm, ottenuto sommando i 5 valori delle altezze e dividendo per 5. Infatti 5 sono le modalità ma i ragazzi sono 18. Bisogna quindi tenere conto del relativo "peso", ossia del fatto che 172 incide più degli altri dati perché più frequente. Pertanto dobbiamo calcolare prima la somma di tutte 18 le altezze, nel modo seguente:
168 × 3 + 169 × 4 + 170 × 4 + 171 × 2 +172 × 5 = 3062
Adesso dividiamo questo valore per 18, ottenendo l'altezza media, cioè circa 170,1 cm.
DEFINIZIONE Data una distribuzione statistica numerica di cardinalità finita diciamo media aritmetica ponderata o pesata delle sue modalità, il numero ottenuto dal rapporto fra la somma delle differenti modalità, ciascuna moltiplicata per la rispettiva frequenza, e la somma delle frequenze. |
Vediamo ancora un esempio.
Nella seguente tabella sono riportati i pesi, in kg, rilevati a pazienti durante una visita medica, suddivisi in classi arbitrarie di peso. Vogliamo determinare il peso medio del generico paziente.
Peso (in Kg.) |
48 – 52 |
53 – 59 |
60 – 63 |
64 – 69 |
70 – 73 |
74 – 80 |
Numero di pazienti |
2 |
4 |
3 |
5 |
8 |
2 |
Dato che le modalità non sono numeri ben stabiliti ma classi, dobbiamo scegliere per ciascuna un rappresentante. In questi casi, di solito, si sceglie l’elemento centrale, così la nostra distribuzione si trasforma nella seguente.
Peso (in Kg.) |
50 |
56 |
61,5 |
66,5 |
71,5 |
77 |
Numero di pazienti |
2 |
4 |
3 |
5 |
8 |
2 |
Ecco l'istogramma relativo.
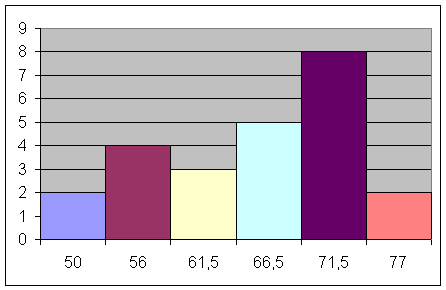
Il peso medio è
![]()
Non sempre la media aritmetica, semplice o ponderata, è un valore soddisfacente a rappresentare l’intera distribuzione., nel senso che non sempre ci fornisce buone informazioni.
Per esempio se in un gruppo di 5 ragazzi tutti alti 160 cm, inseriamo un ragazzo estremamente alto, per esempio 200 cm, la media da 160 cm, passa a più di 166 cm. In questo modo quindi si eleva di ben 6 cm l'altezza media e 6 cm su 160 sono ben il 3,75%. In questo modo però 5 ragazzi hanno un'altezza che è di 6 cm più bassa di quella media e il sesto ha un'altezza che è più elevata della media di circa 34 cm. Non possiamo perciò considerare la media aritmetica come un buon rappresentante dell'altezza media dei 6 ragazzi.
Ciò accade sempre con la media aritmetica, ossia l'introduzione di valori molto estremi conduce a risultati spesso lontani dalla realtà.
In questo caso potrebbe essere conveniente ordinare i ragazzi per altezza e prendere l'elemento che in qualche modo divide i ragazzi in due gruppi ugualmente numerosi. Poniamo una definizione.
DEFINIZIONE Data una distribuzione statistica numerica di cardinalità finita, ordiniamo le modalità in maniera crescente. Diciamo mediana della distribuzione il numero che si ottiene nel seguente modo
|
Con riferimento all'esempio precedente, essendo 6 i ragazzi considereremo il terzo e il quarto, entrambi alti 160 cm, ed effettueremo la media aritmetica delle loro altezze, ottenendo ovviamente ancora 160 cm.
Che informazione ci fornisce la mediana? Ci dice che almeno la metà dei ragazzi ha un'altezza che non è superiore a 160 cm e almeno metà ha un'altezza che non è inferiore a 160 cm.
Un ulteriore indice centrale è il seguente.
DEFINIZIONE Diciamo moda di una distribuzione statistica di cardinalità finita, le modalità che presentano la massima frequenza. Una distribuzione con una sola modalità a cui corrisponde la massima frequenza si dice unimodale, con due bimodale e così via; in generale una distribuzione con più di una moda si dice plurimodale. |
Quindi nel caso delle altezze, possiamo dire che la moda è 160 cm.
In generale quando tutte le modalità hanno la stessa frequenza o vi sono molte mode, questo indice non è significativo e perciò si preferisce non considerarlo.
La moda si usa soprattutto nei sondaggi d’opinione. Non è casuale infatti, la scelta di questo nome per l'indice definito: il termine moda è strettamente collegato allo stesso termine usato nel linguaggio quotidiano ed è in qualche modo la traduzione del modo di dire: “la maggioranza ha sempre ragione”. Con la moda si determina appunto la “tendenza” della maggior parte degli intervistati.
Come si vede ognuno dei tre indici fornisce un'informazione di tipo diverso. Risulta quindi interessante considerarli tutti e tre per ottenere più informazioni possibili. Anzi conviene considerare anche indici che non sono centrali, ma che sono simili alla mediana.
DEFINIZIONE Data una distribuzione statistica numerica di cardinalità finita, ordiniamo le modalità in maniera crescente. Diciamo quartili della distribuzione i tre numeri che dividono la distribuzione in 4 parti ugualmente numerose. |
Ovviamente il secondo quartile coincide con la mediana. In questo caso il primo quartile ci dice come si comporta il primo 25% della distribuzione, il terzo come si comporta l'ultimo 25%.
Per esempio considerando i dati ISTAT relativi al consumo energetico medio per abitante nei capoluoghi di provincia italiani nel 2003, si trova che il primo quartile è circa Kwh 1046,2, la mediana circa Kwh 1147,8 e il terzo quartile Kwh 1237,3, mentre la media aritmetica è circa Kwh 1155,4. Ciò significa che in media ogni abitante ha consumato Kwh 1155,4, ma il 25% degli abitanti ha consumato meno di Kwh 1046,2 e il 25% più di Kwh 1237,3, infine la metà ha consumato meno di Kwh 1147,8 e l'altra metà più di questo valore.
Dato che 1155,4 – 1046,2 = 109,2 e 1237,3 – 1046,2 = 191,1, possiamo dire che la distribuzione non è molto simmetrica, nel senso che non possiamo dire che mediamente tutti hanno consumato la stessa energia, ma una parte di popolazione ha consumato molto più di quanto un'analoga parte ha "risparmiato".