DISPERSIONE
Gli ultimi esempi ci spingono a studiare il comportamento della distribuzione da altri punti di vista, a considerare per esempio l’ampiezza della distribuzione, cioè la differenza fra il valore massimo e quello minimo.
DEFINIZIONE Data una distribuzione statistica a valori numerici, diciamo suo rango la differenza fra i valori massimo e minimo che essa presenta. |
A cosa può servire conoscere il valore del rango di una distribuzione?
Un valore relativamente piccolo (rispetto ai valori in gioco), ci suggerisce che la distribuzione è “abbastanza” uniforme, ossia che i suoi valori differiscono poco fra loro; un valore elevato non dà nessuna informazione specifica.
Consideriamo la seguente distribuzione che si riferisce alla misurazione dello spessore, espressa in mm, di un campione di 8 circuiti elettronici.
0.23 |
0.25 |
0.24 |
0.26 |
0.23 |
0.22 |
0.25 |
0.27 |
Il rango appare particolarmente piccolo, appena
(0.27 – 0.22) mm = 0.05 mm.
Determiniamo la media del campione
Vediamo che il rapporto del rango con la media è
0,05/0,24375 » 20 %
Come si nota un valore abbastanza grande.
Consideriamo invece, la seguente distribuzione relativa a 10 rilevamenti effettuati nell'arco di una giornata, del prezzo, espresso in euro, dell’azione di una società quotata in borsa.
122.3 |
122.8 |
123.1 |
122.9 |
123.2 |
123.5 |
123.3 |
123.0 |
122.4 |
122.6 |
Il rango vale
(123.5 – 122.3) € = 1.2 €.
che è molto più grande in valore assoluto del precedente, ma il suo valore relativo è molto più piccolo; infatti la media è
e il rapporto appena
1,2/122,91 » 0,97% .
Torniamo a chiederci quale sia il migliore indice centrale.
È evidente che in una distribuzione uniforme, nella quale tutti i valori sono uguali, uno qualunque dei tre indici può considerarsi come rappresentante; non è così in una distribuzione in cui vi è concentrazione massima, cioè in cui tutti i valori, tranne uno, sono nulli. Una buona idea è allora quella di introdurre un nuovo concetto che misuri in qualche modo quanto ciascun valore differisce da quello che abbiamo indicato come rappresentante della distribuzione.
DEFINIZIONE Data una distribuzione statistica formata da n elementi che indichiamo genericamente con xi e la cui media è x, diciamo suo scarto semplice medio la quantità dove il simbolo delle barre verticali indica che il valore dell’espressione in esso contenuta viene considerato sempre positivo ossia si considera il suo valore assoluto. |
Cerchiamo di capire perché abbiamo considerato i valori assoluti degli scarti.
Cominciamo a calcolare lo scarto semplice medio della distribuzione:
(1, 1, 1, 2, 2, 3, 3, 4, 5, 6),
la cui media vale
Si ha, considerando i valori assoluti
e senza i valori assoluti
![]() .
.
Quel che abbiamo ottenuto nell’esempio precedente non è un caso, ma un fatto generale. Vale infatti il seguente risultato.
TEOREMA Data una distribuzione statistica di media x , la somma delle differenze delle singole modalità con x , vale zero. In simboli: |
Nella tabella seguente sono riportate le variazioni percentuali dei prezzi al consumo, calcolati dall'ISTAT nel mese di gennaio di ogni anno e considerati rispetto allo stesso mese dell'anno precedente.
Anno |
Variazione anno precedente |
1997 |
+2,6 |
1998 |
+1,6 |
1999 |
+1,3 |
2000 |
+2,1 |
2001 |
+3,1 |
2002 |
+2,3 |
2003 |
+2,7 |
2004 |
+2,0 |
2005 |
+1,6 |
2006 |
+2,2 |
Calcoliamo la variazione media nel periodo 1997 –2006.
![]()
Quindi in media ogni anno i prezzi al consumo sono aumentati del 2,15% rispetto all'anno precedente.
Vediamo quanto ogni singolo valore si discosta da questa media
![]()
Quindi lo scarto semplice medio è di ben 0,43, valore molto alto, perché confrontato con la media è
![]() .
.
Definiamo adesso una quantità che misura meglio la dispersione della distribuzione.
DEFINIZIONE Diciamo scarto quadratico medio di una distribuzione statistica formata da n elementi, ognuno dei quali è indicato genericamente con xi e la cui media è x , la quantità DEFINIZIONE Diciamo varianza di una distribuzione statistica, il quadrato dello scarto quadratico medio. |
Calcoliamo lo scarto quadratico medio della distribuzione dell’esempio precedente
![]()
Rimane sempre il problema di stabilire il significato dello scarto quadratico medio. Consideriamo allora un’altra grandezza.
DEFINIZIONE Diciamo coefficiente di variazione di una distribuzione statistica formata da n elementi, ognuno dei quali è indicato genericamente con xi, la cui media è x e il cui scarto quadratico medio è s, la quantità s/x . |
Calcoliamo il coefficiente di variazione della precedente distribuzione
Abbiamo
![]() .
.
Pertanto anche con lo scarto quadratico medio stabiliamo che in genere la media aritmetica non è un buon indice centrale per la distribuzione dei prezzi al consumo, dato che in media ciascun dato annuo differisce dalla media del 25% circa.
In generale possiamo dire che se la distribuzione è uniforme, allora sia lo scarto semplice sia lo scarto quadratico medio sono nulli, perché i dati non presentano variabilità, se invece siamo nel caso in cui le n modalità di una distribuzione statistica sono tutte nulle tranne una che assume valore uguale a k, si ha
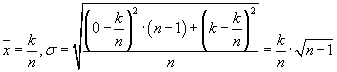
Quindi più vicino a zero è il valore di s e più uniforme è la distribuzione, migliore è la media come suo rappresentante.
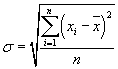 .
.