Le operazioni fra insiemi
Prima di definire delle vere e proprie operazioni fra insiemi, chiediamoci
come possiamo rappresentare graficamente due insiemi.
Riflettiamo un attimo, da un punto di vista grafico due curve chiuse come possono essere disegnate? È semplice capire che se esse sono diverse sono possibili solo i tre casi seguenti:
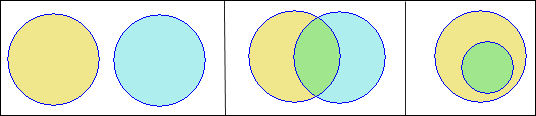
Cioè le due curve possono
1. non avere punti in comune
2. avere alcuni punti in comune e altri no
3. tutti i punti di una sono anche punti dell’altra.
La prima operazione che definiamo riguarda la determinazione degli eventuali elementi comuni a due insiemi.
Definizione Diciamo intersezione di due o più insiemi l'insieme formato dagli elementi a essi comuni. Indichiamo l'intersezione con il simbolo: Ç. |
Così se A = {1, 2, 3} e B = {2, 3, 4, 5}, avremo
A Ç B = {2, 3};
mentre se A = {1, 2, 3} e B = {2, 3}, avremo
A Ç B = {2, 3} = B.
Cosa accade se però gli insiemi non hanno elementi in comune, come nel caso, ad esempio, dell'insieme dei numeri pari e di quello dei numeri dispari?
Definizione L'intersezione di due insiemi A e B privi di elementi comuni, individua l’insieme vuoto. In questo caso gli insiemi si dicono fra loro disgiunti. L’insieme vuoto si indica con uno dei seguenti simboli: { }, Æ. |
Così se A = {1, 2, 3} e B = { 4, 5}, avremo
A Ç B = { } = Æ.
Ovviamente vale il seguente risultato.
TEOREMA 1 La cardinalità dell'intersezione di due o più insiemi è un numero non negativo non superiore alla cardinalità dell'insieme con meno elementi. |
Così l'intersezione di un insieme formato da 100 elementi con uno formato da 43 elementi e con uno formato da 71 elementi, è un insieme di cardinalità compresa tra 0 e 43. In simboli:
|A| = 100, |B| = 43, |C| = 71 Þ 0 ≤|A Ç B Ç C| ≤ 43.
Definiamo un'altra operazione.
Definizione Diciamo unione di due o più insiemi, l'insieme i cui elementi appartengono ad almeno uno degli insiemi componenti. Indichiamo l'unione con il simbolo: È. |
Così se A = {1, 2, 3} e B = { 4, 5}, avremo
A È B = {1, 2, 3, 4, 5 };
anche se A = {1, 2, 3} e B = {2, 3, 4, 5} avremo
A È B = {1, 2, 3, 4, 5 };
mentre se A = {1, 2, 3} e B = {2, 3}, avremo
A È B = {1, 2, 3} = A.
Anche in questo caso vi è un ovvio risultato.
TEOREMA 2 La cardinalità dell'unione di due o più insiemi è un numero non negativo non inferiore alla cardinalità dell'insieme con più elementi e non superiore alla somma delle cardinalità degli insiemi componenti. |
Così l'unione di un insieme formato da 100 elementi con uno formato da 43 elementi e con uno formato da 71 elementi, è un insieme di cardinalità compresa tra 100 e 100 + 43 + 71 = 214. In simboli:
|A| = 100, |B| = 43, |C| = 71 Þ 100 ≤|A È B È C| ≤ 214.
Definiamo altre due operazioni.
Definizione Diciamo differenza di due insiemi A e B (nell'ordine) l'insieme formato dagli elementi di A che non appartengono a B. Indichiamo la differenza con il simbolo: \. Definizione Diciamo differenza simmetrica di due o più insiemi, l'insieme degli elementi che appartengono a ciascuno degli insiemi componenti ma non alla loro itersezione. Indichiamo la differenza simmetrica con il simbolo: D. |
Come si vede entrambe le operazioni sono delle differenze, solo che nel primo caso abbiamo definito l'operazione solo per 2 insiemi e inoltre togliamo da un insieme gli eventuali elementi comuni ai due insiemi. Nel secondo caso invece la definizione è estesa a più insiemi e gli stessi eventuali elementi comuni vengono tolti dall'unione degli insiemi.
Ovviamente vale il seguente risultato, che si può estendere a un numero qualsiasi di insiemi.
TEOREMA 3 Si ha: A D B = (A È B) \ (A Ç B). |
Così se A = {1, 2, 3} e B = { 4, 5}, avremo
A \ B = { 1, 2, 3} = A, B \ A = {4, 5} = B, A D B = {1, 2, 3, 4, 5 };
se invece A = {1, 2, 3} e B = {2, 3, 4, 5} avremo
A \ B = {1}, B\A = {4, 5}, A D B = {1, 4, 5 };
infine se A = {1, 2, 3} e B = {2, 3}, avremo
A \ B = {1}, B\A = { } = Æ, A D B = {1}.
Anche in questo caso vi sono due semplici risultati.
TEOREMA 4 La cardinalità della differenza degli insiemi A e B, nell'ordine, è un numero non negativo non superiore alla cardinalità di A. La cardinalità della differenza simmetrica di due o più insiemi è un numero non negativo non inferiore alla differenza fra le cardinalità dei due insiemi con più elementi e non superiore alla somma delle cardinalità degli insiemi componenti. |
Così la differenza fra un insieme formato da 100 elementi e uno formato da 43 elementi, è un insieme formato da un numero massimo di 100 elementi; la differenza inversa invece è un insieme formato da un numero massimo di 43 elementi. In simboli
|A| = 100, |B| = 43 Þ 0 ≤|A \ B| ≤ 100, 0 ≤|B \ A| ≤ 43.
La differenza simmetrica fra gli insiemi A e B precedenti, è un insieme che ha un minimo di 100 – 43 = 57 elementi e un massimo di 100 + 43 = 143 elementi. In simboli:
|A| = 100, |B| = 43 Þ 57 ≤|A D B| ≤ 143.
Per vedere una dimostrazione interattiva dei teoremi sulla cardinalità, limitati a 2 soli insiemi, clicca sul seguente pulsante
Avendo definito le operazioni fra insiemi, ci interessa sapere quali proprietà verificano.
TEOREMA 5
Valgono le seguenti uguaglianze (proprietà distributive):
|