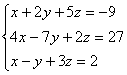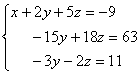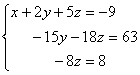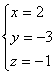|
Metodi di risoluzione dei sistemi lineari
Metodo di
Gauss
Il metodo di Gauss, o di eliminazione successiva delle incognite,
consiste nel trasformare il sistema assegnato in altri equivalenti,
ottenuti mediante combinazioni lineari, in modo da eliminare
un’incognita per volta nelle altre equazioni
|
Esempio: 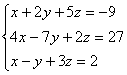
1) Per eliminare l’incognita x dalla
seconda e terza
riga si moltiplica la prima riga per - 4 e si somma
con la seconda riga, si moltiplica la prima riga per
– 1 e si somma con la terza riga, ottenendo
il sistema equivalente
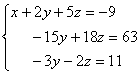 |
2) Per eliminare
l’incognita y dalla terza riga si moltiplica per -5 la terza
riga e si somma alla seconda riga, ottenendo il sistema equivalente
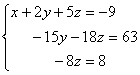
3) Dalla terza
equazione si ricava z = -1, e, sostituendo tale valore nelle altre
equazioni si ottiene la soluzione del sistema
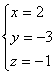 |
Esempio svolto con Excel

Metodo di Jordan
Gauss
Il metodo di
Jordan Gauss o de pivot consiste nel trasformare il sistema in una successione
di sistemi equivalenti, l’ultimo dei quali contiene ciascuna
incognita in equazioni distinte e con coefficiente uguale a 1.
Se il sistema è espresso in forma
matricale il metodo consiste nell’applicare il
procedimento della diagonalizzazione della matrice dei coefficienti
ossia nel trasformare la matrice dei coefficienti in matrice
unità dello stesso ordine.
La soluzione del sistema e’ data dalla colonna dei termini noti.
Osservazione:
Se nelle trasformazioni gli elementi di una riga sono nulli e il termine noto
diverso da zero il sistema è
incompatibile.
|