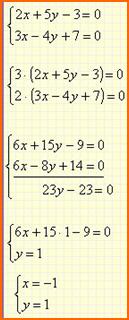|
Metodi di risoluzione di sistemi di due equazioni in due incognite
I metodi di risoluzione di un
sistema di
due equazioni in due incognite sono:
Metodo di sostituzione |
- si risolve
un’equazione rispetto a un'incognita;
- si sostituisce
l'espressione trovata nell’altra;
- si risolve
l’equazione ottenuta, che è in una sola incognita;
- si sostituisce
il valore trovato nell'altra equazione, ricavando il valore
della seconda incognita

|
Metodo di
confronto
-
si risolvono
entrambe le equazioni rispetto alla stessa variabile,
-
si impone che
siano uguali (si confrontano) i secondi membri trovati;
-
si risolve
l’equazione ottenuta, che è in una sola incognita;
-
si sostituisce il
valore trovato nella prima equazione ricavando il valore
della seconda incognita

|
Metodo di
addizione o sottrazione o di riduzione
- si moltiplica una
od entrambe le equazioni per dei fattori non nulli tali che
rendano i coefficienti di un’incognita uguali (od opposti) nelle
due equazioni;
- si
sottrae o si somma (se i coefficienti sono opposti)
membro a membro le due equazioni ottenendo in tal modo
una equazione in una sola incognita;
- si risolve
l'equazione in una sola incognita;
- si sostituisce il
valore dell'incognita trovata in una delle due equazioni
iniziali
|
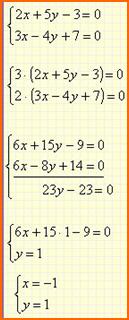
|
Metodo di Cramer
Il metodo consiste nel calcolare il
determinante, D, costituito dalle colonne dei coefficienti
delle incognite e i determinanti dell’incognita x, Dx, ottenuto
sostituendo la colonna dei coefficienti della x con quella dei
termini noti, e il determinante dell’incognita y, Dy, ottenuto
sostituendo la colonna dei coefficienti della y con quella dei
termini noti
 
|