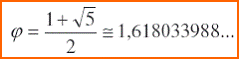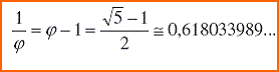|
I conigli di Fibonacci
Leonardo da Pisa, meglio
conosciuto come Fibonacci, (“Filius Bonacci”),
è un illustrissimo matematico del XIII
secolo, che deve la sua notorietà alla famosa serie numerica di cui
porta il nome, la cosiddetta "serie di Fibonacci”.
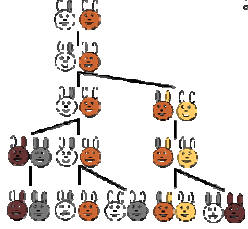
I numeri di Fibonacci sono stati introdotti come soluzione del
problema di modellare la crescita di una popolazione di conigli in
n mesi, ipotizzando che ogni coppia di conigli impieghi un mese per
diventare adulta, e un secondo mese per procreare un’altra coppia.
La successione dei numeri di Fibonacci è una
successione ricorsiva lineare e omogenea, definita nel modo
seguente:
 ; ;
 ; ;

ogni termine è somma dei due termini che lo precedono: 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, 233, etc.
Proprietà
- la somma di dieci numeri consecutivi della
successione è divisibile per 11;
- sommando più numeri consecutivi della serie e
aggiungendo ulteriormente "1", si ottiene un altro numero di
Fibonacci che nella sequenza segue di due posti l'ultimo addendo;
Es. 1+1+2+3+5+1 =13, ossia il settimo numero della sequenza
- dividendo un qualsiasi numero per il penultimo numero
che lo precede nella sequenza, si ottiene come quoziente 2 e come
resto il numero precedente il divisore;
Es. 34=13*2+8
- il quadrato di qualsiasi numero della serie è uguale
al numero che lo precede, per il numero che lo segue, più o meno 1;
Es.82=64 64=5*13-1
- il massimo comune divisore di due numeri di Fibonacci
è ancora un numero di Fibonacci;
- la somma dei quadrati di due numeri consecutivi della
successione è uguale al numero che occupa il posto ottenuto dalla
somma dei posti dei numeri considerati;
Es. 32 + 5 =34 ossia il posto n° 9 nella serie
- il rapporto fra un numero e il suo precedente, per n
che tende all’infinito, è pari al
rapporto aureo, golden ratio, 1,618;
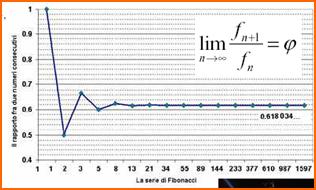
- il rapporto fra un numero e il suo successivo, per n che tende
all’infinito, è pari a 0,618;
- molti numeri della successione sono primi, il più grande è il 571-esimo
con 119 cifre;
- l’unico numero quadrato presente nella successione è 144;
- l’unico numero cubico presente nella successione è 8.
Osservazioni
Nella serie di Fibonacci all’aumentare di n il rapporto
tra ogni termine ed il suo precedente tende a
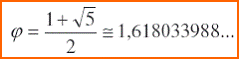
e
all’aumentare di n il rapporto tra ogni termine ed il
termine
seguente tende a
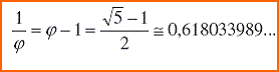
|
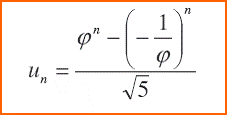
Il matematico De
Moivre (1667-1754) trovò una
formula per
determinare l’n-esimo termine della successione di
Fibonacci:
|
.
|