Vogliamo considerare enti particolari relativi allo studio della geometria del triangolo.

Definizione.
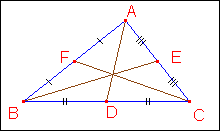
Diciamo mediana relativa a un lato di un triangolo il segmento che ha per estremi il punto medio del lato e il vertice a esso opposto.

Definizione.
Diciamo altezza relativa a un lato di un triangolo il segmento che ha per estremi il vertice opposto al lato e il piede della retta perpendicolare condotta da quel vertice alla retta a cui appartiene il lato.

Definizione.
Diciamo bisettrice di un angolo interno di un triangolo il segmento che ha per estremi il vertice dell’angolo e l’intersezione della semiretta che divide l’angolo in due parti congruenti, con il lato opposto all’angolo.

Teorema 1.
I punti della bisettrice di un angolo sono equidistanti dai lati dell’angolo.

Teorema 2.
Il luogo geometrico dei punti del piano equidistanti dagli estremi di un segmento è la retta perpendicolare al segmento e passante per il suo punto medio. Questo luogo viene detto asse del segmento.

Teorema 3.
Le bisettrici degli angoli interni di un triangolo si incontrano in uno stesso punto, detto incentro, che è il centro della circonferenza inscritta nel triangolo (ossia della circonferenza tangente a ciascun lato del triangolo).

Teorema 4.
Gli assi dei lati di un triangolo si incontrano in uno stesso punto, detto circocentro, che è il centro della circonferenza circoscritta al triangolo (ossia della circonferenza passante per i vertici del triangolo).

Teorema 5.
Il segmento che unisce i punti medi di due lati di un triangolo è parallelo al terzo lato e misura quanto metà di esso.

Teorema 6.
Le mediane dei lati di un triangolo si incontrano in uno stesso punto, detto baricentro, che divide ciascuna mediana in due parti, di cui quella che contiene il vertice è doppia dell’altra.

Teorema 7.
Le altezze dei lati di un triangolo si incontrano in uno stesso punto, detto ortocentro.

Teorema 8.
Le bisettrici di due angoli esterni di un triangolo e dell’angolo interno a essi non adiacente si incontrano in uno stesso punto, detto excentro.