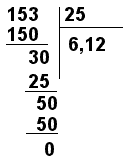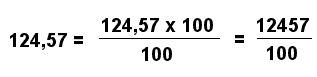Abbiamo definito numero razionale l'insieme di tutte le frazioni equivalenti a una data frazione. Per esempio il numero 1/2 è l'insieme {1/2, 2/4, 3/6, ...}. Poiché una frazione indica il risultato di una divisione tra numeri interi, possiamo rappresentare un numero razionale utilizzando proprio la divisione. In particolare se il resto della divisione di due numeri interi è diverso da zero, cioè se il dividendo non è multiplo del divisore conveniamo di "continuare" la divisione con il seguente procedimento. Poniamo una virgola dopo il quoziente, moltiplichiamo il resto per dieci e lo dividiamo per il divisore iniziale, scriviamo il quoziente di questa divisione dopo la virgola. Se il resto è di nuovo diverso da zero, ripetiamo il procedimento descritto. Fin quando continueremo questo procedimento? Consideriamo cosa può accadere dopo un numero finito di passi, inferiore al valore del divisore:
Come possiamo essere sicuri di ottenere un resto già ottenuto dopo un numero finito di passi, inferiore al valore del divisore? Perché, con riferimento all'esempio, i resti possibili nella divisione per 22 sono 0, 1, 2, 3, ..., 20, 21. Quindi dopo al massimo 22 divisioni dobbiamo ottenere un resto già ottenuto in precedenza, ma ciò significa che a quel punto, continuando la divisione, otterremo sempre la stessa successione di resti e quindi la stessa successione di cifre nel quoziente. Con riferimento all'esempio otterremo sempre i resti 18 e 4 e di conseguenza nel divisore le cifre 8 e 1, quindi la divisione avrà come quoziente 9,681818181.... Tenuto conto di quanto abbiamo visto possiamo affermare quanto segue: Definizione a1a2...an,b1b2...bmc1c2...cpc1c2...cpc1c2...cp...., in cui ciascun simbolo rappresenta una delle dieci cifre 0, 1, 2, …,9. A seconda del risultato della divisione distinguiamo diversi numeri razionali. Definizione 1. un numero intero se tutte le cifre b1b2...bm e tutte le cifre c1c2...cp sono uguali a zero; 2. un numero decimale limitato se almeno una delle cifre b1b2...bm è diversa da zero e tutte le cifre c1c2...cp sono uguali a zero; 3. un numero periodico semplice di periodo c1c2...cp se tutte le cifre b1b2...bm sono uguali a zero e almeno una delle cifre c1c2...cp è diversa da zero; 4. un numero periodico misto di periodo c1c2...cp e antiperiodo b1b2...bm se almeno una delle cifre b1b2...bm e almeno una delle cifre c1c2...cp sono diverse da zero. Per indicare che un numero ha un certo periodo, le cifre del periodo vengono scritte solo la prima volta che si ripetono e vengono indicate con una linea sopra il periodo. Il numero razionale rappresentato dalla frazione 232/99, in forma decimale si rappresenta con il numero periodico semplice q = 2,34343434... che scriviamo in modo più compatto Il numero razionale rappresentato dalla frazione 8679/3700 si rappresenta con il numero periodico misto q = 2,34567567567… che indichiamo brevemente con Vale il seguente risultato. Teorema 1 Il seguente esempio giustifica il teorema. Abbiamo moltiplicato per 100 per eliminare le cifre decimali. Se avessimo avuto n cifre decimali avremmo moltiplicato numeratore e denominatore per 10n. Vale anche quest'altro risultato. Teorema 2 Anche in questo caso proponiamo un esempio. Abbiamo moltiplicato per (1000 - 1), in modo da ottenere due numeri che hanno lo stesso periodo, 478, che nella sottrazione si elimina. Se avessimo avuto un periodo di n cifre decimali avremmo moltiplicato numeratore e denominatore per (10n - 1). Si ha infine Anche in questo caso proponiamo un esempio a giustificazione del teorema. Abbiamo moltiplicato per (1000 - 10), in modo da ottenere due numeri che hanno lo stesso periodo, 34, che nella sottrazione si elimina. Se avessimo avuto un periodo di n cifre decimali e un antiperiodo di m cifre, avremmo moltiplicato numeratore e denominatore per (10n - 10m). Un'altra cosa interessante da osservare è che abbiamo difficoltà ad esprimere l'insieme Q dei numeri razionali sotto forma di successione ordinata. Infatti, a differenza di quanto accade nell’insieme dei numeri interi, nell’insieme Q non esiste il concetto di successivo e di precedente. Cioè, dati due numeri razionali relativi, scritti sotto forma di frazioni o di numeri decimali, siamo in grado di confrontarli, ossia di dire se sono uguali o, in caso negativo, quale dei due sia maggiore, ma non siamo in grado di trovare il successivo di un numero razionale. Ci spieghiamo meglio: il successivo del numero naturale 7 è 8 perché fra i due numeri non vi sono altri numeri naturali. Il successivo del numero decimale 12,3 non esiste perché, per esempio, fra 12,3 e 12,4 ci sono infiniti altri numeri (p.e. 12,33331; 12,30000001; ecc..). e questo discorso vale per qualunque altra coppia di numeri razionali venga scelta. Definizione L'insieme dei numeri naturali e quello dei numeri interi relativi sono insiemi discreti. |