L’area
della superficie laterale di un prisma retto è uguale al prodotto della
misura del perimetro di base per la misura dell’altezza del prisma.Indicando con Sl l'area della superficie laterale del prisma retto, con h la misura della altezza e con p la misura del perimetro di base, si ha: Sl = p∙h.
Detta Sb l'area di una base, l'area della superficie totale St si ottiene con: St = Sl + 2∙Sb.
Il volume di un prisma retto si calcola moltiplicando l'area di base per l'altezza: V = Sb∙h
Se indichiamo con
a, b, c
le misure delle tre dimensioni del parallelepipedo rettangolo,
osserviamo che: due facce hanno ciascuna l’area uguale al prodotto a·b;
altre due facce hanno ciascuna l’area uguale al prodotto a·c;
e infine altre due facce hanno ciascuna l’area uguale al prodotto b·c.L'area della superficie totale si calcola con:
St = 2(ab+ac+bc).
Il volume si calcola moltiplicando l'area di base per l'altezza: V = Sb ∙h.
L’area
della superficie totale di un cubo si trova moltiplicando per 6 l’area
di una faccia.
da cui si ricava:
.Il volume del cubo, come per il prisma retto, si calcola moltiplicando l'area di base per l'altezza; in questo caso l'area di base è pari a
e l'altezza vale
, pertanto si ha:
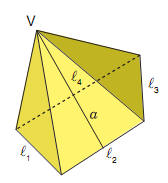L’area
della superficie laterale di una piramide retta è uguale al semiprodotto
della misura del perimetro di base per la misura dell’apotema della
piramide:
L'area della superficie totale è:
Dal momento che una piramide è equivalente alla terza parte di un prisma di base e altezza congruente a quelle del prisma, segue che il volume della piramide è dato dalla formula:
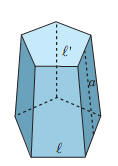L’area
della superficie laterale del tronco di piramide regolare è uguale al
prodotto della semisomma delle misure dei perimetri delle due basi, p e
p', per la misura dell’apotema a:
L'area della superficie totale è:
.Il volume del tronco di piramide si ottiene dalla formula:
