Cilindro

L'area della superficie laterale di un cilindro si ottiene moltiplicando la misura della circonferenza di una base per la misura dell'altezza del cilindro. Da questa proprietà segue che, se indichiamo con r la misura del raggio di base, con h quella dell'altezza, l'area della superficie laterale del cilindro è espressa dalla formula:
Aggiungendo le aree dei due cerchi di base si ottiene l'area della superficie totale del cilindro:

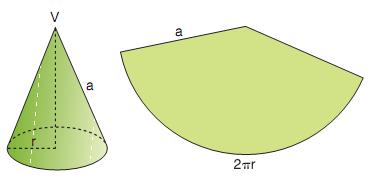
Cono

L'area della superficie laterale di un cono di raggio r è uguale alla misura di mezza circonferenza di base moltiplicata per la misura a dell'apotema:  .
L'area della superficie totale si ottiene aggiungendo ad l'area di base:

Tronco di cono

L'area della superficie laterale del tronco di cono definito dai raggi r e r', dall'apotema a e dall'altezza h, si calcola con la formula: . L'area della superficie totale si ottiene con la formula:

Sfera

L’area di una superficie sferica è uguale al quadruplo di quella di un suo cerchio massimo: .
Riscrivendo la formula:, si deduce facilmente che una superficie sferica è equivalente alla superficie laterale del cilindro a essa circoscritto.


Se poi si calcola il rapporto della superficie sferica e della superficie totale del cilindro circoscritto, si trova:

Da ciò si deduce che il rapporto della superficie sferica e della superficie totale del cilindro a essa circoscritto è 2/3, come il rapporto dei corrispondenti volumi (teorema di Archimede).