POLIGONO

Definizioni  
 
  • Si chiama poligono la figura formata da una poligonale semplice e dalla parte di piano da essa limitata.
  • Un poligono si dice convesso se rimane dalla stessa parte rispetto alla retta di ogni suo lato.
  • Un poligono si dice concavo se il prolungamento di qualche suo lato taglia il poligono.
In un poligono convesso (figure 1 e 2) si chiamano:
  • angoli interni: gli angoli convessi che hanno gli stessi vertici del poligono e per lati le semirette contenenti due lati consecutivi;
  • angoli esterni: gli angoli adiacenti agli angoli interni del poligono;
  • corda: ogni segmento che unisce due punti del contorno appartenenti a lati diversi;
  • diagonale: ogni segmento che ha per estremi due vertici non consecutivi;
  • perimetro: un segmento uguale alla somma dei suoi lati.


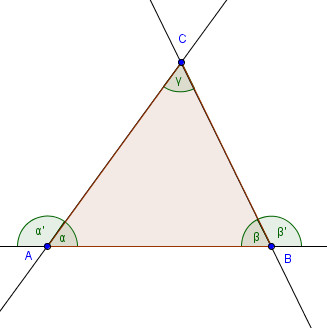
fig.1



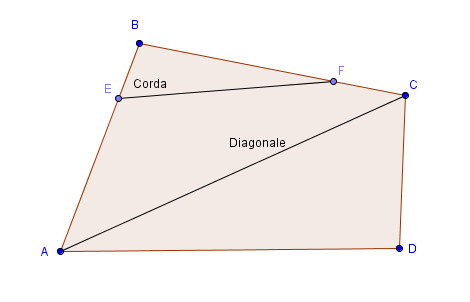
fig.2

 

Definizione  
  Un triangolo è un insieme di punti del piano costituito da una poligonale chiusa di tre lati e dai suoi punti interni. Un triangolo si può anche definire come intersezione di tre angoli convessi che hanno i vertici in tre punti non allineati.

In ambiente GeoGebra dobbiamo osservare che l'oggetto poligono deve essere costruito utilizzando l'apposito strumento, poiché non basta disegnare una poligonale chiusa, formata da segmenti distinti, che racchiuda una regione convessa di piano.
Quando un poligono è costruito correttamente, esso viene riempito di colore e considerato un unico oggetto. Diversamente, una spezzata chiusa formata da semplici segmenti è interpretata come un insieme di oggetti distinti. Per renderci conto di questa differenza, proviamo a trascinare un segmento qualsiasi della figura ABCD e un lato del poligono EFGH nella finestra sottostante.

  Questa è un'Applet Java creata con GeoGebra da www.geogebra.org - Java non risulta installato sul computer in uso - fare riferimento a www.java.com


ATTIVITÀ
  1. Traccia un poligono convesso di 6 lati, traccia le sue diagonali e gli angoli esterni.
  2. Traccia un poligono convesso φ di 5 lati. Con lo strumento Punto medio o centro, individua i punti medi dei lati di φ. Costruisci il poligono che ha i vertici nei punti trovati.
  3. Cliccando sul poligono con lo strumento Distanza o lunghezza, visualizza la misura del perimetro.
    Cliccando sul poligono con lo strumento Area, visualizza l'area.
  4. Il rapporto tra il perimetro di un poligono ω1 e il perimetro del poligono ω2 , che ha i vertici nei punti medi dei lati di ω1, è costante? Se si trascinano i vertici di ω1 il rapporto cambia?