CALCOLO DI π
Poligoni inscritti in una circonferenza
Il
perimetro 2p
di un poligono regolare inscritto
nella circonferenza costituisce una approssimazione della misura γ
della circonferenza stessa.
Poiché la misura della circonferenza si calcola con
la formula
possiamo
affermare che
, da cui si ricava che
.
L'approssimazione migliora al crescere del numero di lati del
poligono regolare considerato. Ci proponiamo allora di trovare la
formula che genera la successione dei perimetri dei poligoni regolari
in funzione del numero n
dei lati.
Consideriamo
il triangolo equilatero ABC, inscritto in una circonferenza di raggio
unitario.
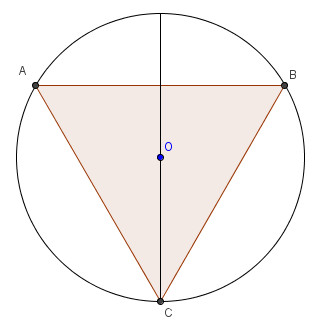
fig. 1.
Il
lato AB misura
e il semiperimetro è
,
pertanto si calcola:
.
Calcoliamo la misura del lato dell'esagono regolare considerando la figura 2.
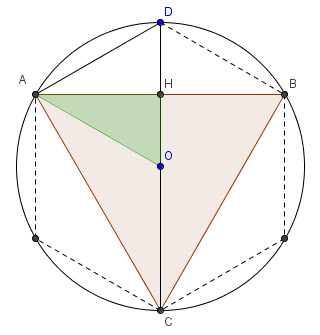
fig. 2
Per
il primo teorema di Euclide, applicato al triangolo CAD, sappiamo che
.
Questa
relazione contiene due incognite:
e
.
La lunghezza del segmento DH può essere calcolata per
differenza:
.
La misura del segmento OH si ottiene applicando il teorema di
Pitagora al triangolo rettangolo AOH. In formule si scrive:
,
quindi
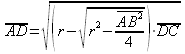
Ponendo:
,
e sapendo che
si ottiene:
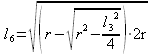
Da questo risultato possiamo intuire la generalizzazione della formula che, a partire dalla conoscenza della misura del lato del poligono regolare di n lati, calcola la misura del lato del poligono regolare di 2n lati in funzione del raggio della circonferenza circoscritta:
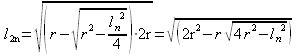
Se la circonferenza ha
raggio unitario,
r
= 1 e la formula diventa:
Siamo allora in grado di generare gli elementi della successione, definita per ricorrenza, formata dai lati dei poligoni regolari:
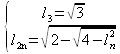con
n = 3, 6, 12, 24, 48, ...
A questo punto possiamo utilizzare il foglio di calcolo di GeoGebra per determinare gli elementi della successione, calcolare i perimetri dei poligoni regolari inscritti nella circonferenza di raggio unitario e determinare le approssimazioni di π.
Attivata la voce Visualizza Foglio di calcolo, dal menu Visualizza, scegliamo, dal menu Opzioni, Arrotondamento a 15 cifre significative (fig. 3)
fig. 3.
Nel Foglio di Calcolo si inseriscono le formule seguenti:
A2:
3
A3: =A2*2
A4: =A3*2
....
B2:
=sqrt(3)
B3: = sqrt(2-sqrt(4-B2^2))
B4: =
sqrt(2-sqrt(4-B3^2))
.....
C2:
=A2*B2
C3: =A3*B3
....
D2:
= C2/2
D3: = C3/2
----
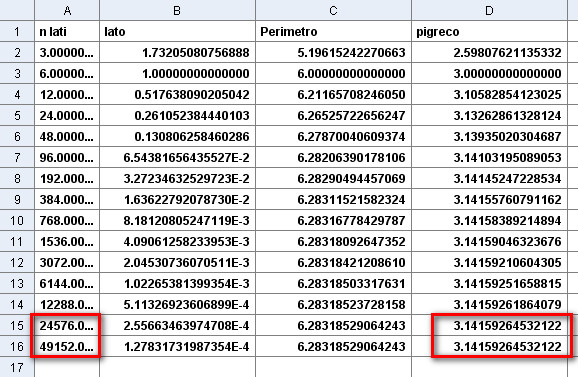
fig.
4
I risultati ottenuti sono corretti solo fino alla settima cifra decimale (3,1415926 4532122) a causa degli errori di arrotondamento che il computer inevitabilmente introduce. Anche la modalità di scrivere la formula nella colonna B influenza l'efficienza e la precisione del calcolo.
Il valore corretto di π, calcolato alle prime 50 cifre decimali, è: 3.14159265358979323846264338327950288419716939937510...
ATTIVITĀ
Studiare i perimetri dei polinomi regolari circoscritti a una circonferenza di raggio unitario e costruire la successione che approssima il valore di π.