Definizione
Se a e u sono due segmenti fra loro
commensurabili, si chiama misura di a rispetto a u,
preso come unità di misura, il numero razionale positivo o
nullo![]() per il quale risulta
per il quale risulta![]() .
.
MISURA DEI SEGMENTI
| Definizione | |
|
Due segmenti x e u si dicono:
|
Quando due segmenti a e u sono commensurabili vale la seguente definizione.
|
Definizione |
|
|
|
Se a e u sono due segmenti fra loro
commensurabili, si chiama misura di a rispetto a u,
preso come unità di misura, il numero razionale positivo o
nullo |
Nel caso di due segmenti a e u che siano fra loro
incommensurabili, vale la seguente definizione.
|
Definizione |
|
|
|
Si chiama misura di un segmento a incommensurabile con l'unità di misura u il numero irrazionale positivo individuato dalle due classi numeriche che contengono, rispettivamente, le misure approssimate per difetto e per eccesso di a rispetto a u. |
Diremo allora che, fissata l'unità di misura, ogni segmento
ha una sua misura, che è un numero razionale non negativo se
il segmento è commensurabile con l'unità di misura, mentre è
un numero irrazionale positivo nel caso sia incommensurabile.
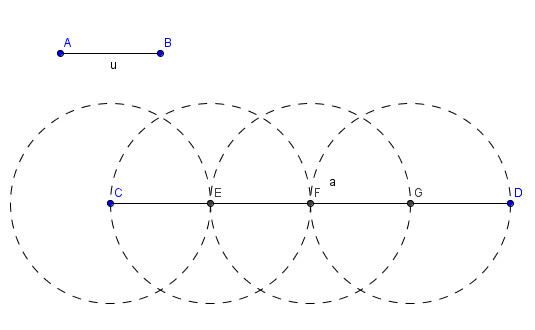 Sia
CD commensurabile con AB.
Sia
CD commensurabile con AB.
Per misurare il segmento CD, fissata
l'unità di misura u, si prende il compasso con apertura AB, si
punta in C e si interseca il segmento AB in E; con la stessa apertura
si punta in E e si interseca CD in F e così via. Poiché
i due segmenti sono commensurabili, si troverà un'ultima
circonferenza che interseca CD proprio nel punto D. La misura di
CD
rispetto ad AB è data dal numero di circonferenze tracciate,
ovvero dal numero di volte che il segmento CD contiene AB.
Quando l'unità di misura scelta e il segmento da misurare sono incommensurabili si verifica la situazione della figura seguente.
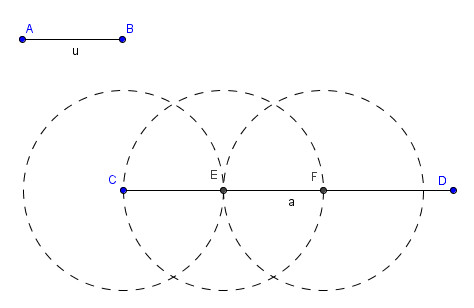 E'
importante notare che nessun sottomultiplo di u consentirà di
costruire un numero intero di circonferenze che intersecano CD
secondo la costruzione illustrata nel caso precedente. In questo
consiste il significato di incommensurabilità.
E'
importante notare che nessun sottomultiplo di u consentirà di
costruire un numero intero di circonferenze che intersecano CD
secondo la costruzione illustrata nel caso precedente. In questo
consiste il significato di incommensurabilità.
In questi casi non resta che cercare la misura approssimata, per eccesso o per difetto, del segmento dato. Per costruire la successione delle approssimazioni occorre creare dei sottomultipli dell'unità di misura. Possiamo procedere semplicemente dividendo a metà il segmento AB e, se non basta, dividendo ulteriormente tale segmento applicando la costruzione.
COSTRUZIONE
Facendo doppio click nella finestra seguente, si apre il foglio completo in GeoGebra.
Occorre ricordare che, quando la misura viene condotta con uno strumento informatico, i valori rappresentati sono sempre una approssimazione razionale del risultato esatto. L'aritmetica del computer è una aritmetica finita: con essa si possono rappresentare solo numeri razionali con un numero di cifre decimali limitato.
Per renderci conto di questo fatto è sufficiente provare a
eseguire alcuni calcoli con il foglio di calcolo di GeoGebra.
Dopo
aver scelto l'opzione Arrotondamento di 15 cifre significative,
costruiamo la successione, definita per ricorrenza,![]() e
calcoliamo i rapporti
e
calcoliamo i rapporti![]() .
Nella colonna B della figura seguente si nota che talvolta accade che i
rapporti calcolati risultino erroneamente identici; infatti:
.
Nella colonna B della figura seguente si nota che talvolta accade che i
rapporti calcolati risultino erroneamente identici; infatti:
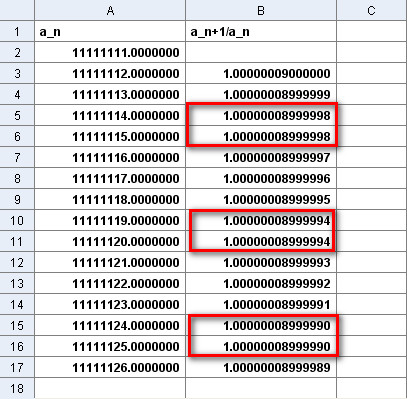
![]() ma
in entrambi i casi GeoGebra fornisce 1.00000008999998;
ma
in entrambi i casi GeoGebra fornisce 1.00000008999998;
![]() ma
viene dato lo stesso risultato 1.00000008999994;
ma
viene dato lo stesso risultato 1.00000008999994;
![]() ma
il risultato calcolato è sempre 1.00000008999990.
ma
il risultato calcolato è sempre 1.00000008999990.
Queste
incongruenze sono inevitabili e sono generate dalla rappresentazione
finita dei numeri nel sistema hardware (non è un difetto del
software). Per poter calcolare un più elevato numero di cifre
decimali corrette, oltre le 15 tipiche di un processore a 32 bit, è
necessario ricorrere ad algoritmi specifici, ovvero a programmi
appositamente creati per superare le limitazioni intrinseche
dell'unità aritmetico logica del calcolatore.