TRAPEZIO   

Definizione  
  Si chiama trapezio ogni quadrilatero convesso che ha due lati opposti paralleli.
Teorema  
  In un trapezio gli angoli adiacenti a un lato obliquo sono supplementari.
Definizioni  
 
  • Un trapezio si dice rettangolo se ha un lato obliquo perpendicolare alle due basi.
  • Un trapezio si dice isoscele se ha i lati obliqui congruenti.

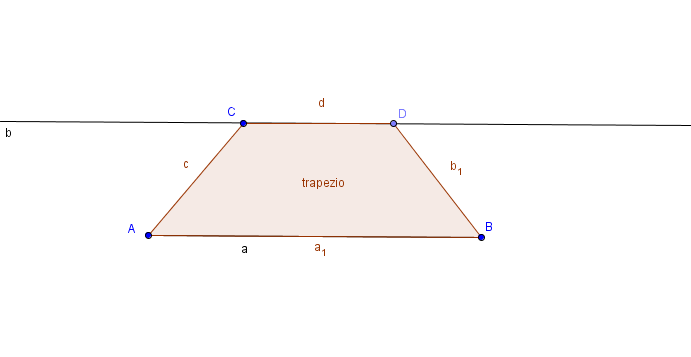
COSTRUZIONE

Per costruire un trapezio, tenendo conto della definizione, occorre costruire due segmenti paralleli (le basi) e quindi tracciare i lati obliqui.
Con GeoGebra, possiamo utilizzare lo strumento retta parallela e seguire il protocollo di costruzione illustrato qui sotto.

GeoGebra Vista grafica

N. Nome Definizione Comando
1 Punto A    
2 Punto B    
3 Segmento a Segmento [A, B] Segmento[A, B]
4 Punto C    
5 Retta b Retta per C parallela a a Retta[C, a]
6 Punto D Punto su b Punto[b]
7 Quadrilatero trapezio Poligono A, B, D, C Poligono[A, B, D, C]
7 Segmento a1 Segmento [A, B] di Quadrilatero trapezio Segmento[A, B, trapezio]
7 Segmento b1 Segmento [B, D] di Quadrilatero trapezio Segmento[B, D, trapezio]
7 Segmento d Segmento [D, C] di Quadrilatero trapezio Segmento[D, C, trapezio]
7 Segmento c Segmento [C, A] di Quadrilatero trapezio Segmento[C, A, trapezio]

 

ATTIVITÀ

  1. Costruire un trapezio qualsiasi con riga e compasso secondo la procedura di costruzione della retta parallela senza utilizzare lo strumento Retta Parallela.
  2. Costruire un trapezio rettangolo utilizzando i pulsanti Retta per due punti e Compasso.
  3. Costruire un trapezio isoscele.
  4. Tracciare nella Vista Grafica due segmenti congruenti e due segmenti diseguali; costruire il trapezio isoscele che ha per lati i quattro segmenti dati.
  5. Costruire un trapezio isoscele applicando le proprietà di simmetria.