fig.1
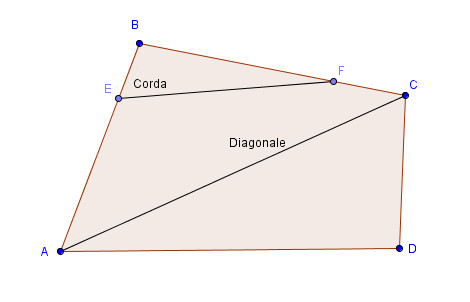
fig.2
POLIGONI
| Definizioni | |
|
|
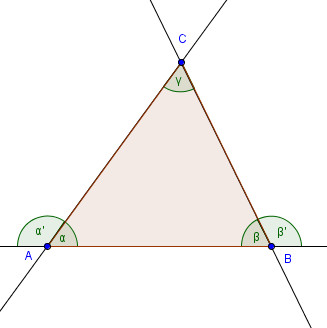
In un poligono convesso (figure 1 e 2) si chiamano:
|
|
|
|
| Definizione | |
| Dati i tre punti non allineati A, B, C, si chiama triangolo ABC la figura costituita dall'intersezione dei tre angoli convessi ABC, BCA, CAB, ciascuno dei quali ha per vertice uno dei punti dati e ha i lati che passano per gli altri due. |
In ambiente GeoGebra dobbiamo osservare che l'oggetto poligono deve essere
costruito utilizzando l'apposito strumento, poiché non basta disegnare una poligonale chiusa, formata da segmenti distinti,
che racchiuda una regione convessa di piano.
Quando un poligono è costruito correttamente, esso viene riempito di colore e
trattato come un unico oggetto. Diversamente, una spezzata chiusa formata da
semplici segmenti è interpretata come un insieme di oggetti distinti. Per
renderci conto di questa differenza, proviamo a trascinare un segmento qualsiasi
della figura ABCD e un lato del poligono EFGH nella finestra sottostante.