|
Cubo
|
Il volume del parallelepipedo rettangolo è dato dal prodotto delle
misure delle sue tre dimensioni:
V = a
·b·c.
In particolare, il volume del
cubo di spigolo l si calcola con: V = l3. |
|
Prisma
|
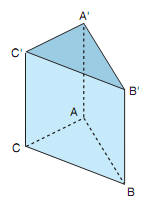
Poiché
un prisma è equivalente a un parallelepipedo rettangolo, di
base equivalente e altezza uguale, il volume del prisma si
calcola con: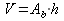
|
|
Piramide
|

Dal
momento che una piramide è equivalente alla terza parte di
un prisma di base e altezza rispettivamente uguali, segue che il
volume della piramide è dato dalla formula: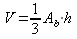
|
|
Tronco di piramide
|
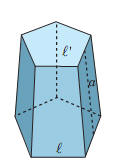
Se
indichiamo con A e
A¢
le aree delle due
basi, il volume V
del tronco di piramide
è dato dalla
formula:
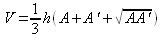
|
|
Cilindro
|
 Poiché
un cilindro è equivalente a un prisma di base equivalente e
altezza uguale, la formula Poiché
un cilindro è equivalente a un prisma di base equivalente e
altezza uguale, la formula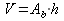 ,
che dà il volume del prisma, dà anche quello del
cilindro. ,
che dà il volume del prisma, dà anche quello del
cilindro.
Tenuto
poi conto che l’area di base di un cilindro di raggio r
è 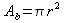 ,
si deduce che il volume del cilindro, di raggio r
e
altezza h,
è dato dalla formula: ,
si deduce che il volume del cilindro, di raggio r
e
altezza h,
è dato dalla formula: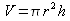
|
|
Cono
|
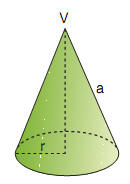
Essendo
il cono equivalente a un terzo di un cilindro di ugual raggio e
altezza uguale, segue che il volume del cono, di raggio r e
altezza h, è dato dalla formula: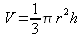 . .
|
|
Tronco di cono
|
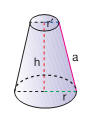 Quanto
al tronco di cono si può provare, con il principio di
Cavalieri, che: «Un tronco di cono e un tronco di
piramide, con le rispettive altezze uguali e basi
rispettivamente equivalenti, sono equivalenti».
Dopo di che, essendo: Quanto
al tronco di cono si può provare, con il principio di
Cavalieri, che: «Un tronco di cono e un tronco di
piramide, con le rispettive altezze uguali e basi
rispettivamente equivalenti, sono equivalenti».
Dopo di che, essendo: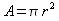 ; ;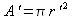 ; ;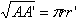 ,
il volume si calcola con la formula: ,
il volume si calcola con la formula:
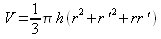
|
![]()



 Poiché
un cilindro è equivalente a un prisma di base equivalente e
altezza uguale, la formula
Poiché
un cilindro è equivalente a un prisma di base equivalente e
altezza uguale, la formula
 Quanto
al tronco di cono si può provare, con il principio di
Cavalieri, che: «Un tronco di cono e un tronco di
piramide, con le rispettive altezze uguali e basi
rispettivamente equivalenti, sono equivalenti».
Dopo di che, essendo:
Quanto
al tronco di cono si può provare, con il principio di
Cavalieri, che: «Un tronco di cono e un tronco di
piramide, con le rispettive altezze uguali e basi
rispettivamente equivalenti, sono equivalenti».
Dopo di che, essendo: