fig. 1
PRINCIPIO DI CAVALIERI
|
Definizione |
|
|
|
Due
solidi che hanno uguale estensione si dicono equivalenti. |
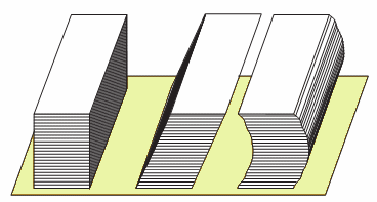
Si consideri un parallelepipedo rettangolo formato da un certo numero di fogli di carta, rettangolari, tutti uguali tra loro e sovrapposti esattamente l’uno all’altro (fig. 1).
Facendo scorrere lievemente i fogli l’uno sull’altro si può deformare il parallelepipedo e trasformarlo in un altro parallelepipedo non più retto o anche in un solido con le facce incurvate, pur lasciando in ogni caso invariate la base e l’altezza.

fig. 1
È
evidente che i tre solidi, essendo costituiti dallo stesso numero di
fogli, sono equivalenti, cioè hanno la stessa estensione.
Possiamo così giustificare, intuitivamente, il seguente
assioma che costituisce il principio di Cavalieri:
|
Assioma |
|
|
|
Due solidi che si possono collocare in modo che siano equivalenti le loro sezioni con un qualsiasi piano parallelo a un piano fisso sono equivalenti. |
Applicando il principio di Cavalieri è possibile dimostrare i seguenti casi notevoli di equivalenza tra solidi.
Prismi con basi equivalenti e altezze uguali sono equivalenti.
Un prisma qualunque è equivalente a un parallelepipedo rettangolo avente altezza uguale e base equivalente.
Un cilindro è equivalente a un prisma avente altezza uguale e base equivalente.
Ogni prisma è equivalente al triplo di una piramide avente base e altezza uguali a quelle del prisma considerato.
Un cono è equivalente a una piramide avente altezza uguale e base equivalente.
Un cono è equivalente alla terza parte di un cilindro avente base e altezza rispettivamente uguali.