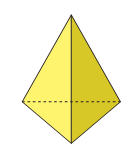
È limitato da 4 triangoli equilateri congruenti; ha 6 spigoli e 4 vertici. È una piramide regolare a base triangolare.
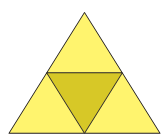
Lo sviluppo della sua superficie è un triangolo equilatero con il lato doppio dello spigolo del tetraedro.

Questo poliedro non è altro che il cubo.
Ha per facce 6 quadrati congruenti, 8 vertici e 12 spigoli.
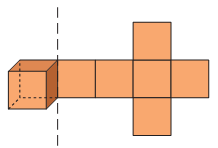
Sviluppo della superficie di un cubo.
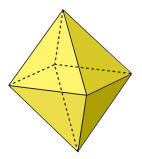
È limitato da 8 triangoli equilateri congruenti; ha 6 vertici e 12 spigoli. Può considerarsi come l’insieme di due piramidi quadrangolari regolari che hanno la base in comune e sono situate da parti opposte rispetto a essa.
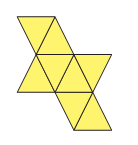
Sviluppo della superficie di un ottaedro regolare.
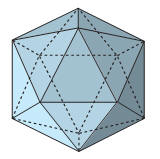
È limitato da 20 triangoli equilateri congruenti; ha 12 vertici e 30 spigoli.
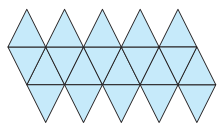
Sviluppo della superficie di un icosaedro regolare.
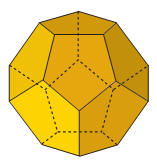
È limitato da 12 pentagoni regolari congruenti; ha 20 vertici e 30 spigoli.
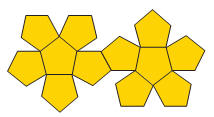
Sviluppo della superficie di un dodecaedro regolare.