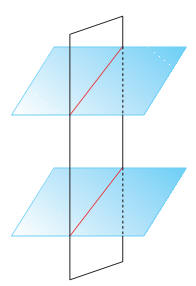
 fig. 1
fig. 1- Per un punto dello spazio si può condurre uno e un solo piano parallelo a un piano dato
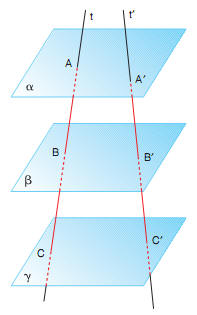 fig. 2
fig. 2
- Tre o più piani paralleli staccano sopra due trasversali qualunque segmenti corrispondenti in proporzione ( fig. 2).
SPAZIO
| Assioma | |
Ogni piano
a
dello spazio divide l’insieme degli
ulteriori suoi punti in due parti non vuote, tali che:
|
|
| Definizioni | |
| Si chiama semispazio la figura costituita da un piano a e da una delle due parti in cui a divide lo spazio. |
RETTE
| Definizioni | |
|
|
|
|
|
PIANI
Poiché per tre punti non allineati passa uno e un solo piano, allora due piani distinti nello spazio non possono avere in comune tre punti non allineati. I casi che si possono quindi presentare come possibili sono i seguenti:
| Definizioni | |
|
|
|
|
| Teorema | |
| Se due piani distinti hanno in comune due punti A e B, allora hanno in comune tutta la retta AB e solo questa retta. |
PROPRIETÀ
 fig. 1 fig. 1 |
|
 fig. 2 fig. 2 |
|