Teorema di Eulero

  

 

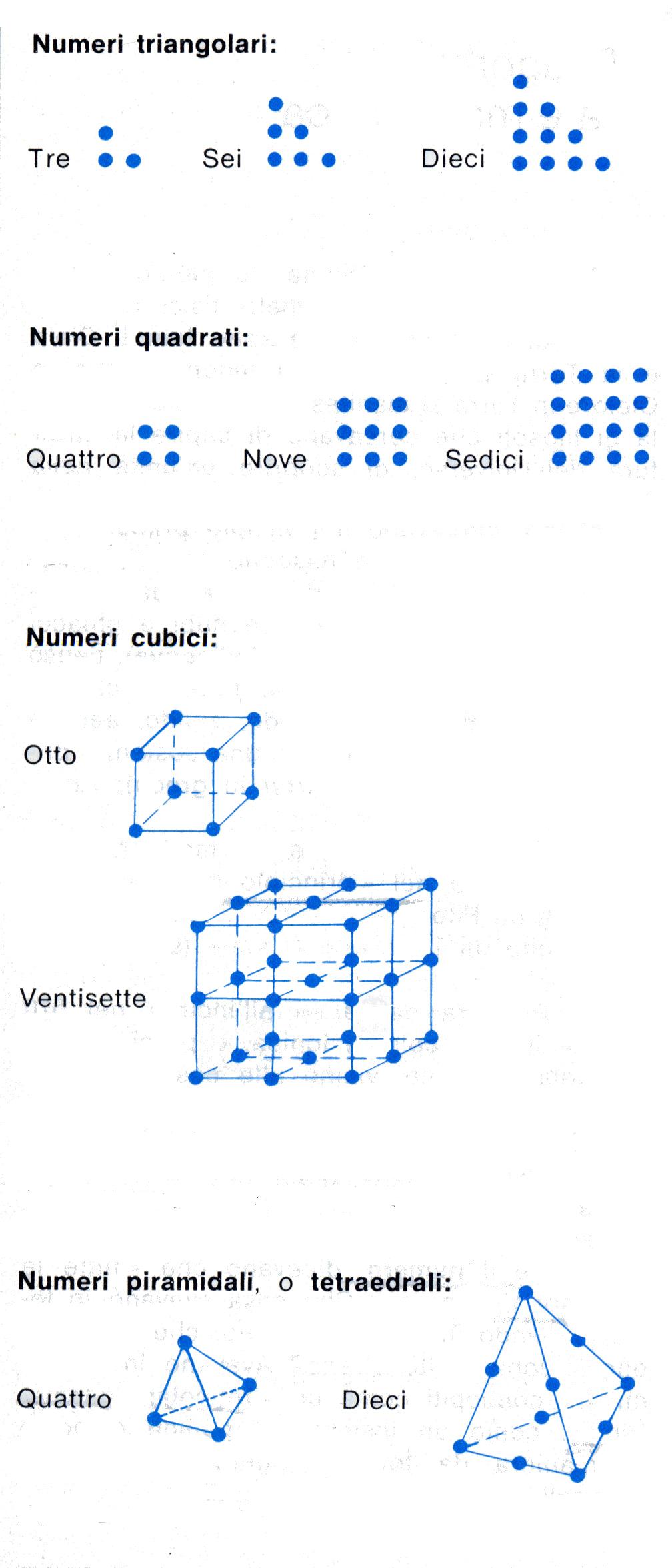
I pitagorici ritenevano i numeri naturali l’essenza delle cose, la chiave di interpretazione del misterioso universo; cogliendo in essi un ordine di armoniose perfezioni. Essi rappresentavano i numeri mediante punti detti monadi (unità), indivisibili (atomi), ma non evanescenti, dotati di dimensioni piccolissime, e raggruppati in modo da formare figure geometriche. Così, i numeri 1, 3, 6, e 10 erano detti triangolari perché i corrispondenti punti potevano essere disposti a triangolo; i numeri 1, 4, 9, 16 venivano chiamati numeri quadrati perché intesi come punti che potevano essere disposti in un quadrato; i numeri 8, 27, 64 venivano chiamati numeri cubici, perché intesi come punti che potevano essere disposti in un cubo; i numeri 4, 10, 20 venivano chiamati numeri piramidali perché i corrispondenti punti potevano essere disposti in una piramide.

Proprietà dei numeri pitagorici

  • Ogni numero naturale dispari è uguale alla differenza di due quadrati dei due numeri consecutivi di cui il numero dato è uguale alla somma

 

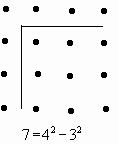
  • La somma di una successione di numeri dispari consecutivi dà sempre un numero quadratico

.

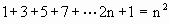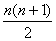
  • un numero triangolare è uguale alla somma dei numeri naturali che lo precedono. Poiché i numeri naturali costituiscono una progressione aritmetica di ragione 1, l’ennesimo numero triangolare è

Osservazioni:

i numeri triangolari sono presenti anche nel triangolo di Pascal: la terza diagonale è costituita dalla sequenza dei numeri 1, 3, 6, 10, 15, 21….

 

 

binomi 1a