Un'equazione di Pell - Eulero è un'equazione diofantea quadratica in due variabili, del tipo:

x² − dy²=1  oppure x² − dy²= −1

Una soluzione banale dell’equazione del primo tipo, valida per ogni valore di d, è

                                              x = ± 1, y = 0.

Le equazioni del primo tipo possono avere soluzioni intere per ogni valore di d che non sia un quadrato perfetto; quelle del secondo hanno invece soluzione soltanto per alcuni casi particolari.
L’equazione del tipo x² − dy²=1 (con d numero naturale non quadrato perfetto), nota come equazione di Pell-Eulero, fu studiata da grandi matematici quali Fermat, Wallis, Eulero e Lagrange.
Il nome dell’equazione deriva da quello del matematico inglese John Pell, al quale Eulero attribuì il metodo per trovarne le soluzioni.
Solo in tempi recenti utilizzando sofisticati software si è pervenuto ad una soluzione del problema dei buoi: il valore di d corrisponde ba 4729494, e la soluzione minima dell’equazione , ossia nell’insieme 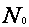, è rappresentata da un numero di oltre duecentomila cifre dell’ordine di cifre. Sbalorditiva come mandria!

Osservazione

Il numero  è un numero inimmaginabile in quanto non è direttamente raffrontabile con alcunché di fisico.