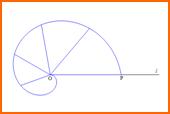Teorema di Eulero

 

Nel suo libro "Sulle spirali", Archimede dà una descrizione cinematica della curva: la spirale è la traiettoria descritta da un punto che si muove con velocità uniforme su una semiretta che ruota uniformemente intorno al polo.
L’equazione polare della spirale archimedea è:
Modificando il parametro a, la spirale ruoterà, mentre il parametro b controlla la distanza tra i bracci, che per tale spirale è sempre costante.

Osservazioni

  • La spirale di Archimede presenta due bracci, uno per θ > 0 e l'altro per θ < 0, ed entrambi si congiungono nel polo.

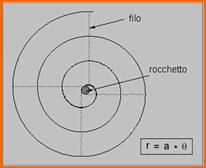
  • la spirale di Archimede è detta evolvente perché ha le spire equidistanti.



  • Si può ipotizzare tale spirale come un sottile filo avvolto su un rocchetto; dove r corrisponde alla lunghezza del filo srotolato dal rocchetto e la circonferenza di quest’ultimo corrisponde alla distanza fra le spire.

                                                                        
Applicazioni:

  • nella vita reale la spirale di Archimede si trova nella traccia dei dischi in vinile, nelle pompe di scorrimento per liquidi e gas;

  • in medicina il metodo della spirale di Archimede viene utilizzata per misurare una disfunzione motoria nella malattia di Parkinson.

Curiosità

  • Xah Lee diede un’interpretazione artistica alla spirale archimedea


Spirale di Archimede